Things don't quite add up

[thegreger]

Hi all,

I realize that there are multiple threads on a similar theme to this, but I feel that none of them seem to contain correct information, and most of them don't really deal with the connection to real life.

So I'm trying to model a car that I have access to in real life. Fun, right? Also a path to insanity, apparently. This is going to be a long thread, and potentially a bit interesting to some people and incredibly boring to others. The car is an old MGA race car.

The first thing I did was head out one evening and carry out acceleration tests and coast-down tests on a perfectly straight and flat piece of tarmac (an airplane runway). I'm using a 10 Hz GPS/GLONASS logger, which is typically pretty reliable. I did repeat runs in both directions, and took note of the wind speed at the time (7 m/s, blowing to the northwest, approx. 3-4 m/s in the direction of the runway).

So far, everything makes sense. Let's look at the coast-down tests, convert everything to m/s, and plot the deceleration as a function of speed.

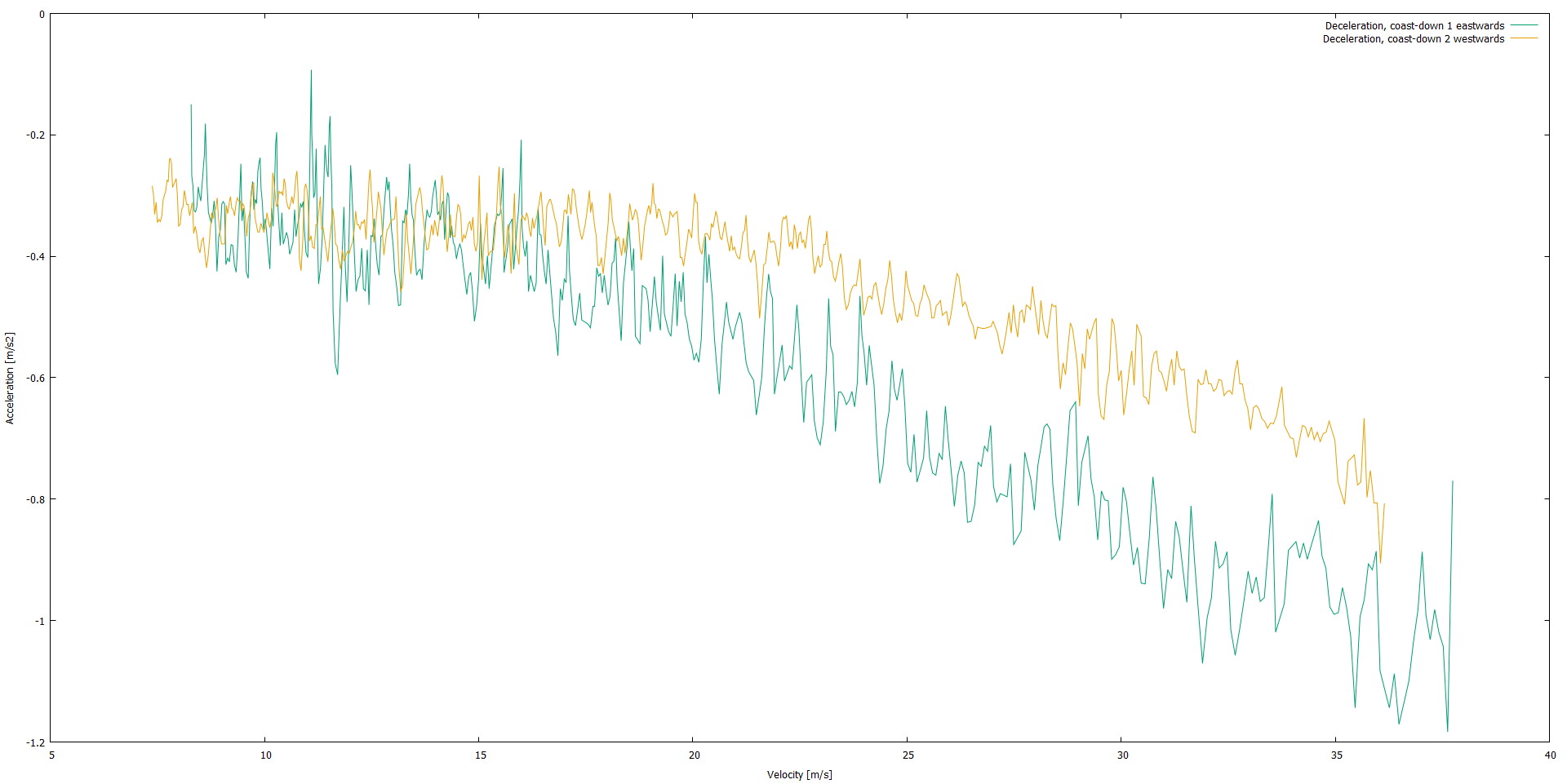
A bit noisy, but that's to expect when looking at any acceleration data derived from speed data. Now, since the wind in the direction of the road was 3-4 m/s, let's add 3.5 m/s to the run with headwind, and subtract 3.5 m/s from the run with tailwind.

Coooool. This data fits a simple mathematical model really well (assuming that 0.5*Cd*A*rho = 0.47, and using a constant rolling resistance of 240 N.

By gently removing some of the noise with a simple low-pass filter, one can then add the decelerating force to the accelerating force (acc and dec data from the same run, to avoid having to correct for wind speed), and calculate wheel HP by the formula P=F*v/745.7. Plotted against engine RPM, we get the following (the dip towards the end is unreliable data, since I release the throttle somewhat while changing gear):

So far, it all makes perfect sense. The MGA engine should be rated at 93 hp SAE gross, which would mean somewhere around 80-ish hp DIN on the crank. 60-65 hp on the wheels is pretty much what you would expect. I repeated these calculations for every run in both directions, and got very consistent results. I will end this post here, and in the next one I want to discuss replicating this data in AC.

 

[thegreger]

Wind speed and coast-down tests

So, to start with I decided to tweak my modded car in order to fit the coast-down test as good as possible. I created a simple perfectly flat and straight track, running from east to west. I changed my car's aero.ini to "SPAN = 1.51", "CHORD = 0.8", "CD_GAIN = 0.91" and set all values in the "body_CD.lut" file to 0.70. This should correspond to a Cd*A of 0.769, or in engineering terms "close enough".

Now the paranormal stuff begins. I know enough about the aero model to have a good starting guess, then I tweaked the rolling resistance in tyres.ini in order to produce reasonable results. I loaded up my flat track, and set the wind speed to 12.5 km/h (3.5 m/s) in Content Manager. I then basically reproduced the run in my first plot above. The blue line below is telemetry exported from AC.

Everything here is almost reasonable. The calculated Cd*A gives a pretty good fit, the rolling resistance seems to make sense. But note how the deceleration in high speeds is too high in the first run (headwind), then too low in the second run (tailwind). This tells me that the Cd*A is correct, since the average deceleration of the two runs would match the average of the real-world data, but that the wind speed doesn't affect the air speed of the car in the way I would expect it to. In fact, in order for the headwind and tailwind coast-down runs to make sense, I would have to dramatically increase the wind speed in AC.

Anyhow, that's not a big deal, since the deceleration data is still very much within a reasonable range. The decelerating force might be off by 5% or so in a given velocity, but it should be a good starting point for the model.

 

[thegreger]

Power curves

Now comes the parts that I really find confusing. I've read elsewhere on this forum that power.lut should be the torque, calculated from wheel hp.

I smoothed out the power curve from my first post (well, actually, I took an average from many runs and then smoothed that). Then I calculated the torque as 9.5488 * 0.7457 * P * N, where P is power in hp (the factor 0.7457 is to convert to kW) and N is rpm. This should be correct according to any sources I can find? I get the same results if I skip dividing by 745.7 when I calculate power in post 1, and just stick to using W (or kW) everywhere.

The power.lut file I get from the wheel hp peaks at about 82 Nm at 4000 rpm (46 hp). Again, according to any info I can find online, torque from wheel hp should be the way to assign values in power.lut. I tested my power.lut file in the AC Torque Helper tool, and it produced the following plot:

Again, this seems reasonable. Remember that this is an engine that should produce approximately 80 hp at the crankshaft, and another identical car has hit 62 wheel hp at a rolling road. Also, remember that the coast-down test indicates that all the decelerating forces are reasonable, if not 100% accurate.

Then comes the final test. Straight-line acceleration, flat ground, both directions. Purple and light blue is from real life, whereas the dark blue curve is from AC.

Now, this is really bad. Note how the real car is aerodynamically limited in the first run (headwind), whereas the AC car seems to be nowhere near its aero limit, despite obviously being way, way low on power. This also supports the idea that I would have to crank the wind speed up to 2-3 times its real value in order to get a realistic wind effect.

Strangely, if I remove the factor 0.7457 in the equation above, I get a pretty good agreement with reality! But then whatever I put in power.lut definitely isn't in Nm. Unless of course it's supposed to be Nm from power measured on the crank, and the 0.7457 is just a pretty close approximation of drivetrain losses? Or is it that I don't understand how to use the "COAST" parameters in engine.ini?

I should add that I have double-checked that I entered the car's mass (in kg, with driver, without fuel) correctly, the gearing and wheel radius is correct (as evident by the speeds that you can see my gear shifts in the plot above) and I haven't got a turbo or anything silly like that. Oh yeah, and I downloaded an app just to check that the wind heading is what I expected it to be, just in case my runway wasn't aligned east-west as I thought.

This is so very, very strange. If the AC model is that low on power, how can it even reach the correct top speed? The decelerating force is definitely not that wrong.

 

[fughettaboutit]

Arch Today at 13:46:
"His torque curve is wrong
If he is accelerating from 3000RPM or something
He assumes it makes 0 torque at 0RPM and scales it to that probably
If someone cares they can sign up and direct him here to CSP discord (invite) then #mod-talk"

 

[thegreger]

Arch Today at 13:46:
"His torque curve is wrong
If he is accelerating from 3000RPM or something
He assumes it makes 0 torque at 0RPM and scales it to that probably
If someone cares they can sign up and direct him here to CSP discord (invite) then #mod-talk"

I agree about this. My way of estimating the car's power curve from its acceleration is not very good, and allows for large errors, but it's best above 3-4000 rpm (at these speeds I get the most consistent results). However, during the acceleration test I never go below 4000 rpm on second gear or higher, so that shouldn't affect the acceleration curves. I've since tweaked the torque curve manually to get the correct acceleration profile, and it's not outrageous, but it's strange that it doesn't match the torque curve I got from the real-life acceleration.

I think that the biggest issue is with the modelling of the retardant force (wind resistance plus rolling resistance). However much I fine tune it, the influence of wind speed relative the ground never quite matches reality. I believe that this is also why I have to have a slightly different torque curve in order to get realistic high-speed acceleration. Also, whatever resistance model AC is using, it seems to fit reality worse than a basic F=Av²+B model.